止まれないキャントストップの勝率: 6,7,8だと5%で一発登頂
tl;dr
- キャントストップのノーストップ戦略の一発登頂確率をDPで求める
- 6,7,8のレーンしか登れない場合,1発で3レーンとも登りきれる確率は5%
前置き
こんにちは.
キャントストップというチキンレースダイスゲームがあります.

4個のダイスと3個のコマ,2から12の数字の書かれたのレーン,11個の自分のビバーク,を使います.
手番では,ダイスを4個ふって2つずつに分けます. そして,2つに分けたそれぞれで出目の合計のレーンのコマを1つ進めます.
例えば出目が「3, 4, 6, 6」であれば 「3+4と6+6」で7と12 のレーンを進められます.9と10のレーンを進めても良いです.
このダイスロールを手番の間,繰り返します.
ただし,1回の手番中で進めることのできるレーンは3つまでです. 4つ目のレーンを進めることはできません.
1つでもレーンを進めることができれば大丈夫ですが, 進める3つのレーンの出目のどれもが作れないとき,バーストになります. 手番中に進んだ分をすべて失います.
例えば,3 と 4 と 5 のレーンを進めている時に「2, 4, 4, 6」という出目が出た場合,3も4も5も作れないのでバーストします.
そうならないように,手番ではダイスを振る前にビバークができます. ビバークをすると手番は終わりますが,そこまでのコマの動きはセーブされ,次の手番からは,ビバークしているレーンではそのマスから進めます. また,バーストしてもビバークは失いません.
最初に3つのコマを登頂させたプレイヤーの勝ちです.
ブラウザでも遊べるのでやりましょう. https://boardgamearena.com/gamepanel?game=cantstop
止まれないキャントストップ
このゲームのロマンは,1手番での完全登頂にあると思います. まさに一発逆転です.
周りからの止まるなという圧力に屈し,自分の自制心を振り切って一切のビバークをしない場合,どのくらいの確率で勝てるのでしょうか.
結果
素朴なDPを書きました.
6,7,8の3つのレーンを登る場合,5%強登れるようです.一番確率が高いです.
[6, 7, 8] [11, 13, 11] => 0.057548888319900036
ただし,6,7,8以外のレーンは登れないものとします.
5%もあるならダイスに祈りを託すには十分な確率な気がします.
久しぶりにDP書いたのでめっちゃバグらせているかもしれません. もしミスってたらこっそり教えて下さい.
コード
全レーンの確率
2,3,12と2,11,12が最も最低の0.0024%の確率で登れます.おとなしくビバークしましょう.
先行研究
1回のロールでの確率: Can't Stop odds
真面目な戦略研究,ルール28: Can't Stop? Try the Rule of 28
JSのArray#shiftが遅いのでキューを頑張る.結果wasmは速い.
JSのArray#shiftはとても遅いです. 後輩がキューを実装したくて困っていました.
キューの実装を紹介して,その計測を示します.
とりあえず計測
高速化の議論をするときは,必ず始めにベンチマークを取りましょう.
shift/pop/spliceを比較しました.ベンチマークは10000要素を1つずつ取り除いていくものです.
const n=100000; arr = Array.from(new Array(n)).map((_,i)=>i) for(let i = 0; i < n; i++){ arr.shift() }
結果
| 実装 | 速度 |
|---|---|
| shift | 1.53 ops/sec ±84.16% |
| pop | 36.88 ops/sec ±2.02% |
| spliceによるshift | 0.94 ops/sec ±161.84% |
| spliceによるpop | 22.37 ops/sec ±2.04% |
shiftは要素数に線形の時間が最悪の場合かかります.この例では,shiftはpopの24倍ほど遅くなりました.
spliceは遅いので使う必要がなさそうです.
キューの実装
このshiftの遅さに耐えられない場合は,キューを自分で実装することになります.
実装はいくつか考えられます.
スタック2つでキュー
スタック2つをキューとして扱う事ができます.
キューを{head:[], tail:[]}と初期化します.
エンキューはtailにpushします.
{head:[], tail:[]}{head:[], tail:[1]}{head:[], tail:[1,2]}{head:[], tail:[1,2,3]}
デキューはheadからpopします. もしheadが空の場合は,tailの要素の順番を逆にしてheadに付け加えます
{head:[], tail:[1,2,3]}{head:[3,2], tail:[]}→ 1{head:[3], tail:[]}→ 2{head:[], tail:[]}→ 3
この実装の計算量は,ならし計算量の問題として有名です. tailの要素の順番を逆にするところで線形時間かかるようにみえます. しかし,操作の回数でならすことで,定数時間となります.
リングバッファ
もし,キューの最大要素数がわかっているなら,リングバッファで実装するのが自然です.
初期化は{data: [?,?,?,?,?], head:0, tail:0}です.
エンキューでは,data[tail]に値を書き込み,tailを1増やします.
このとき,tailが最大要素数より大きいならtailを0とします.
{data: [?,?,?,?,?], head:0, tail:0}{data: [1,?,?,?,?], head:0, tail:1}{data: [1,2,?,?,?], head:0, tail:2}{data: [1,2,3,?,?], head:0, tail:3}
デキューでは,data[head]から値を取り出し,headを1増やします.
このとき,headが最大要素数より大きいならheadを0とします.
{data: [1,2,3,?,?], head:0, tail:3}{data: [1,2,3,?,?], head:1, tail:3}→ 1{data: [1,2,3,?,?], head:2, tail:3}→ 2{data: [1,2,3,?,?], head:3, tail:3}→ 3
計算量は定数です.しかし,この方法は予め要素数がわかっているときしか使えません
このdataは要素数固定なので,ArrayとInt32Arrayの両方で比較しました.
それぞれのキュー実装の計測
それぞれのキューに対してエンキュー75%,デキュー25%の確率(線形合同法)で100000回実行します.
const n = 100000; function zigzag(n, init, shift, push) { let seed = 12345; let size = 0; let last = -1; for (let i = 0; i < n; i++) { if (size > 0 && (seed & 20480) == 0) { // 2^12+2^14=20480 last = shift(init); size--; } else { push(init,seed); size++; } seed = (seed * 1664525 + 1013904223) & 2147483647; } return last; }
結果
Run results for: Queue Implement by 2 Stacks - MeasureThat.net
| 実装 | 速度 |
|---|---|
| 素のArray | 10.24 ops/sec ±2.73% |
| 2スタック | 233 ops/sec ±1.65% |
| リングバッファ | 413 ops/sec ±1.75% |
| リングInt32Array | 417 ops/sec ±2.21% |
予想通りInt32Arrayのリングバッファが一番速いです.
しかし,2スタックの実装も十分に速いです. 要素数が可変というメリットがあるので,キューが必要になった場合は2スタック実装がおすすめです,
おまけ.wasm
高速なキューが必要になるほど複雑なロジックをJSで書くことを諦めましょう.
Rustで書いてwasmにすると 1,725 ops/sec ±1.61% でした. リングバッファの4倍ぐらい速いです.
このMDN通りにすれば,すぐにwasmを使い始められます.
素朴な実装です.
extern crate wasm_bindgen; use wasm_bindgen::prelude::*; use std::collections::VecDeque; #[wasm_bindgen] pub fn zigzag(n: i32) -> i32 { let mut vec = VecDeque::new(); let mut seed = 12345; let mut size = 0; let mut last = -1; for _ in 0..n { if size > 0 && (seed & 20480) == 0 { last = vec.pop_front().unwrap(); size -= 1; } else { vec.push_back(seed); size += 1; } seed = (seed * 1664525 + 1013904223) & 2147483647; } return last; }
unpkgからwasmを読み込む方法です.
(async () => { const importObject = { imports: { } }; const ex = 'https://unpkg.com/@wass80/wasm-queue/wasm_queue_bg.wasm'; const wasm_obj = await WebAssembly.instantiateStreaming(fetch(ex), importObject); const wasm = wasm_obj.instance.exports; window.wasm_zigzag = wasm.zigzag })();
BGAで遊んだボドゲの感想 三密避けてボドゲしたい!
こんにちは.休学しているwassです.
新型コロナの流行っている現在,物理でボドゲするのは困難です.
でも週に1回ぐらいはボドゲしないと死んでしまいますよね?
なので,Board Game Arenaを遊んでいます.
やったボドゲの感想をつらつらと述べていきます.
どれもBGAですぐ遊べるので,気になるゲームがあったら知人とやると良いです.
東海道 4-5人推奨 30分 ★☆☆
物理未プレイ
自分のコマを京都から始めて,東京まで動かす.
まるで,すごろくのようなシステムに見える.

しかし,このゲームはサイコロを振らない.
ゴルフのように最も遅れている人が手番を行う. そして,次の宿屋までの間ならコマをどこまで進めても良い. 止まったところのマスの効果を実行する.
得点の種類はいくつかある. 「温泉に入れば2,3点」「お土産を買えば1,3,5,7点」「寄進をすれば1,2,3点」「風景を集めれば1,2,3,4,5点」「様々ボーナスで3点」
これらの得点を集めて,全員が江戸にたどり着いたとき,最も得点の高い人の勝利である.
感想: このシステム面白くない? 僕にはこれがワーカープレイスメントにみえました.ほしい行動の取り合い,手数の計算.まさにワープレだと思う. ただ,マスの行動ではガチャが多いので,バカヅキして勝ったみたいなことが多くて少し大味かな.
十二季節の魔法使い 4人推奨 90分 ★★☆
物理プレイ済
有名作品.独自の20個の季節ダイスがかっこいいやつ.

ゲーム開始時にこのゲームで使うカードをドラフトする. ラウンドのはじめに季節ダイスをドラフトする. というドラフト大好きゲーム.
基本的にカードを出せば勝利点を得られる. カードを出すためには,4種類の魔力と召喚力が必要になる.それらは季節ダイスから得られる. カードを出せば,追加効果が発生したり,逐次効果が発生したりする.3年後,最も勝利点を得ているのは誰かというゲーム.
魔力をそのまま勝利点に変換する方法もあるので,勝ち筋が複数存在する.
感想: 手札ドラフトがわりと初心者殺しではある. BGAだとなおめんどくさい!
コルト・エクスプレス 5-6人推奨 30分 ★★☆
物理未プレイ
コンポーネントが良い.ナイアガラぐらい好き.

そして内容もナイアガラぐらいタフ. 見た目のギャップは同じぐらいある気がする.
手番では表向きに行動カードを1枚プレイする.もしくは,3枚ドローする. 行動カードは,「移動」「昇降」「拾得」「射撃」「格闘」「保安官」の6種類.
移動して人を殴って落としたお金を拾う,みたいなことをすることになる.
このゲームでは行動カードをプレイしても,直ちに行動するわけではない. 実際にコマに触る前に,ラウンドの指定回数だけ全員が順番に1つの山にカードをプレイする. そして,そのプレイ計画が終わったら,プレイされた順に行動カードをめくって行動を行う.
ラウンド内の人の動きを予想しながら,時には裏向きにプレイされてわからないカードを予想しながら,金をガメていこうというゲームだ.
感想: 計画ゲームを初めてやったんですが面白いですね. 想定通りのことができて嬉しい!というのがわかりやすくて好き.時折,無を殴ることになるけど.
インカの黄金 3-8人 ☆☆☆
物理未プレイ
有名作.やったことがないので遊んだ. 内容は成立しているチキンレースゲーム.

それ以上でもそれ以下でもない.リアルで人を煽りながらするゲームだと思う.
クシディット王国記 90分 4,5人推奨 ★★★
物理未プレイ
計画ゲームが面白かったので,重い計画ゲームもやることにした.十二季節と同じデザイナーである.
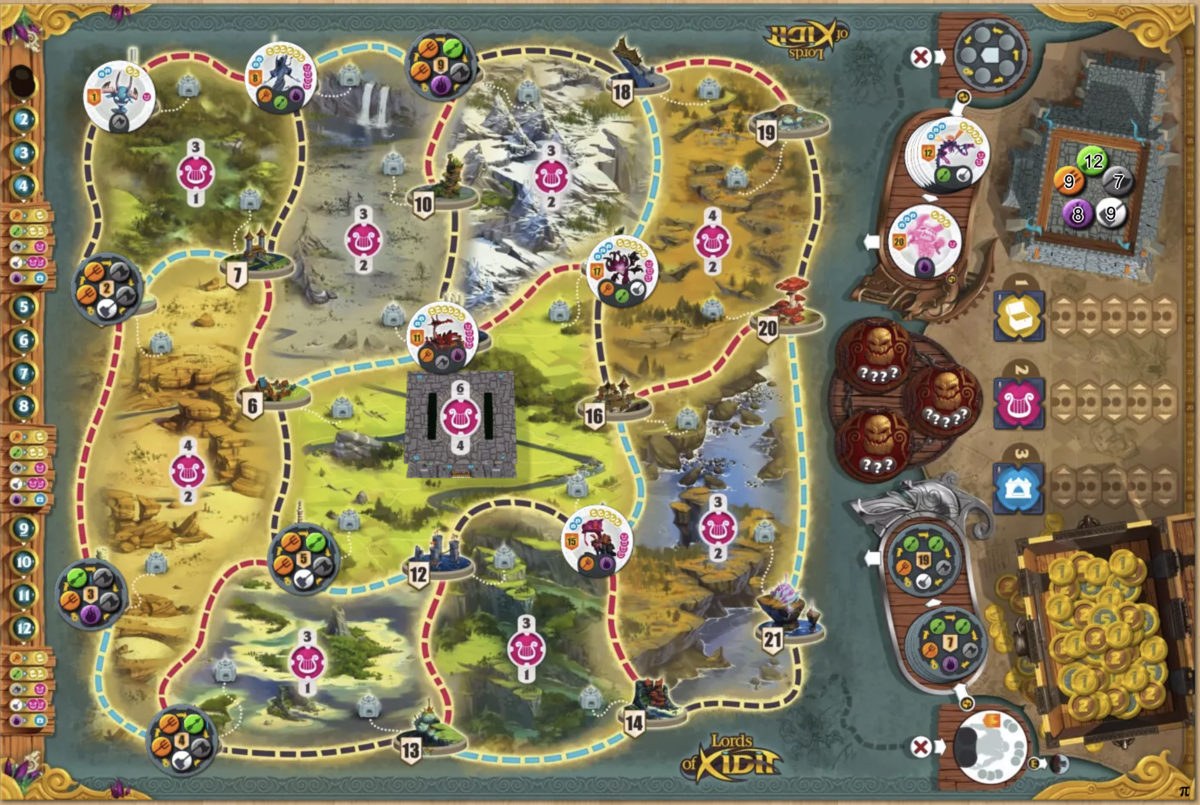
このゲーム,惹かれるギミックが2つある.
1つめは勝利点が3種類存在することだ. お金は合計値で競う.名声はエリアマジョリティで競う.ギルドは早いもの勝ちで競う.
この3種類の要素について,ゲーム開始時にいわば逆辞書順のようなものが決められており,優劣が決定する
例えばお金→名声→ギルドの場合であれば,ゲーム終了時に ,お金が最も少ない1人(もしくは5人なら2人)が脱落し,次に名声が最も少ない人が脱落し,最後にギルドが最も少ない人が脱落する.
残った1人が勝者である.
もう1つのギミックは,この個人計画ボードである.
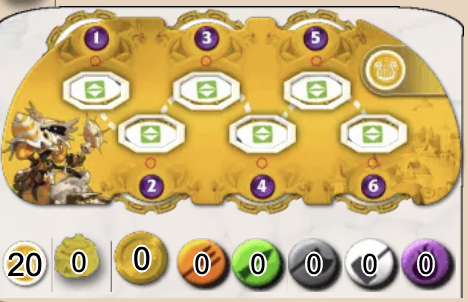
各ラウンドのはじめに,ラウンドで行う6行動を予め計画する. 全員が計画を終えたら1行動ずつ時計回りに実行していく.
行動は5種類しかない.「青の道を行く」「赤の道を行く」「黒の道を行く」「都市行動」「何もしない」
都市の次数は3なので,移動は一意になる. 都市行動も2種類で, 「兵員がいれば兵を1つ補充をする」「敵がいれば兵を消費して勝利点を得る」 のどちらかがほぼ自動的に決定する.
選択が発生するのは少しだけで, 計画をしたらほとんどオートでBGAがやってくれる. ぽこぽこコマが動くのは面白い.
兵や敵は早い者勝ちなので,ここで計画のバッティングが発生する.うまく人の行動の予想しよう.
感想: 計画ゲーム面白いですね.独特な勝利点システムが非常に良いスパイスになっている. コマや都市準備の動きが煩雑なんですが,全部BGAがやってくれるので便利ですね. 物理で持っててもBGAでもやって見る価値のあるゲームだと思います.
1ヶ月間インターンに行ったら寿司を握るのがうまくなった
1ヶ月東京に存在していた間の行動記です。まともなことは書いていないです.
第1週
肉のハナマサ
ホテルにまともなIHとフライパンのあることを確認したので,肉のハナマサで2kg冷凍ミンチを買った。
冷凍みじん切り玉葱とともに電子レンジで温めてキーマカレーを作って食べた。

会社でボドゲした

豊洲を見に行った


豊洲市場でお魚が買えない事実を知らなかったので,晩御飯は手捏ねハンバーグになった

目黒寄生虫館
 愛嬌がある
愛嬌がある
シェアサイクル

便利
塩バジリコ

第2週
味噌ミート

もんじゃ

静止画を眺めるものではない
NHK放送博物館


ピタゴラスイッチのオタクなので,実物展示が良かった
横浜 鎌倉

中華街
 弁財天
弁財天

大仏.小さい.

湘南の海.このあと青豚見た.

江ノ電は人が多すぎてへとへとになった. 湘南モノレールは楽しいジェットコースターだった.
第3週
萩の湯

ピクサー展

インタラクティブなわかりやすく楽しい展示が多くてよかった
寿司

築地で手に入れた寿司ネタを

握る
第4週
風邪を引いた。有給があったので助かった
ハンバーグ

ほやと寿司

ほや美味しいですね.さばくときにめっちゃ水が飛ぶけど.

木の板を買って上に載せたので,クオリティーが10倍になった.
第5週

ボドゲした
休学することにした
こんにちは.
表題の通り,修士課程を休学することにしました. 休学の理由は,なんにもできない気持ちになったからです.
研究があんまりうまく回せず, 他のこともなんにも出来ないみたいな状態が続いてしまっていました.
とりあえず,研究を1ヶ月休んだんですが,あまり何も解決してない気もします. こういうネガティブなこと書いてると, もう一回カウンセリング受けに行ってもいい気がしますね‥
ただ,カウセリングしてもあんまりいい作戦が思い浮かぶわけではないし, 言語化がより進んだという感じもしないです.
親に休学のことを言ったら割とすんなり受け入れてくれたことが,本当に幸いだったと思います. ここでこじれてたらマジで大変だった‥
休学の有効な活用ノウハウとかあったら知りたいです. もしかしたらバイトするかも‥ぐらいのスタンスで居ます.
とりあえず,京都市にパクられた自転車を回収して,休学届を出します.
元気がないみたいな状態ではないので, なんとか生活を生産力に変換する方法を安定させたいです.
登った大文字山です.このまま琵琶湖に抜けました.

東京のレンタルサイクルが好きだ
東京の好きなところがある. 短時間レンタルサイクルが充実していることだ.
東京の都心は,思っているより遥かに狭い. 普段は鉄道や地下鉄でワープのように移動する. しかし,自転車で移動すると意外と狭い事がわかって楽しい.
東京にはものすごい量の自転車レンタルポートがある.

ポートマップ・駐輪 | 東京・港区自転車シェアリング(シェアサイクル)
3コンビニに1つぐらいの感覚である. 全てのポート自転車を借りられるし, どこのポートで乗り捨てても良い. とても便利だ.
東京の道路は自転車に優しい. 京都と違って,車道幅か歩道幅のどちらかは十分にある.しかし,勾配のある坂を上り下りさせられるのが欠点だ.
だが,このレンタルポートで借りられる自転車は電動自転車である. それなりの厳しい坂でも,すいすい登ることが出来る.
借りられる自転車の実装は悪くない.ハードは優秀. 自転車番号をWebから入力. 案内される4桁のPINを入力して解錠. 返却にはポートでロックするだけ. おそらくGPSで位置を取得しているのだろう, ポート内であれば,正常に返却される.
Web側のUIは「駐輪場検索」「自転車番号」の2つある.
駐輪場検索は検索性が悪く使い物にならない.
位置特定して最寄りを出してほしい.

150円/30分という値段も,地下鉄並みで良いと思う. これからも活用していきたい.
ところで,京都でも似たようなサービスが始まった.
こちらも一度使ってみた.
東京に比べてポート数が少ないことが利便性を下げている. これは仕方ない. アプリも使い勝手が悪く,ハードの認識もうまく行かない個体が多かった. Bluetoothで認証させるのがうまく行かないのだろうか. これも仕方ないとする.
肝心の自転車があまりにダメすぎだった. 電気自転車でないことは良い. ハードの認証を駆動させるためにバッテリーが乗っている. ひたすらに重い漕ぎ心地を考えると,そのバッテリーを常時充電しているようである. あまりにひどい. ハードがだめだと,他の改善点が治ってもどうしようもないので悲しんでいる.
京都観光もレンタルサイクルがおすすめなのですが, このサービスはおすすめしません. 電動自転車をレンタルサイクルショップで借りましょう.
定理証明コンテストに参加した [WIP]
TODO多めのまま公開します。別に書いてた下書きが消えたので。
定理証明のコンテストシステムを作って、今日の夕方に第1回のコンテストを開催していた。https://t.co/8vi0dWszRW
— あしぃ (@asi1024) 2019年8月18日
これです。
定理証明コンテストとは,
定理証明支援系を用いて与えられた定理に対して証明を与えるコンテストです。
現在コンテストサイトに実装されている支援系はCoqです。
Coqで解く問題の見た目はこんなかんじです。
Definition task := forall n m, n * S m = n + n * m. Theorem solution: task. Proof. unfold task. (* FILL IN HERE *) Qed.
これはn×(m+1)とn+(n×m)が任意の自然数n,mについて等しいことを示せというものです。
FILL IN HEREの部分にCoqの言葉で証明を与えます。
この問題を通そう
環境準備
Coqのインストールをしたのち,Coqをインタラクティブに使うツールを用意します。
ツールにはEmacs+ProofGeneralが最も標準的です。 WindowsではCoqIDEを使う方法もあります。
vscodeとその拡張vscoqを使う方法も存在したのですが, 現在バグだらけで使い物になりません。 昔のvscodeのバージョンを用いると使えるらしいですが, その方法をおすすめすることはできません。
Emacs+Spacemacs+ProofGeneral導入記事は後で書くことにします。TODO
ここでは他の選択肢として,macでvscode+vscoqを用いる方法を説明します。
初めに brew install coq でcoqを入れます。
そしてここが肝心ですが,vscodeの拡張であるvscoqはすでに更新がされておらず,
最新のvscodeでは正常に動作しません。
なので2年前ぐらいのvscodeをダウンロードして利用しましょう。
Visual Studio Code January 2018
vscodeでvscoq拡張をインストールします。
そうして*.vファイルを開くと,次の証明画面が出ます。
TODO
定義
というわけでこの命題を示しましょう。
forall n m, n * S m = n + n * m.
定理の証明にはまず定義を観察することが大事です。
ドキュメントに定義があります。
Standard Library | The Coq Proof Assistant
https://coq.inria.fr/library/Coq.Init.Datatypes.html#lab1084
また, Coq上でも定義を見ることができます。 TODO
Inductive nat : Set := | O : nat | S : nat -> nat.
natという集合は,次の2つのコンストラクタから生み出されるものである。
と読みます。
例えばOやS (S O)なんかがnatで有ることがわかります。
そして, これが我々の良く知る自然数であるところの0や2に対応しています。
実際に,0や2もcoqで書くことができ,これはcoqではそれぞれOとS (S O)のエイリアスです。
また,+ の定義はaddという関数の糖衣構文で
Fixpoint add n m := match n with | 0 => m | S p => S (p + m) end where "n + m" := (add n m) : nat_scope.
掛け算の定義はmulという関数の糖衣構文で
Fixpoint mul n m := match n with | 0 => 0 | S p => m + p * m end where "n * m" := (mul n m) : nat_scope.
と再帰的に定義されています。
matchは関数型言語ではおなじみのパターンマッチです。
その項のコストラクタによって場合分けを行い, その先の項を返します。
match 項 with | コンストラクタ1 引数1 => 項1 | コンストラクタ2 引数2 => 項2 end
計算の例を示すと,
2+1を計算する例は
S (S O) + S O = add (S (S O)) (S O) = match (S (S O)) with | 0 => (S O) | S p => S (p + (S O)) end = S(S O + S O) ... = S(S(O + S O)) ... = S(S(S(O))
ここで,S (S (S O)) + S Oは(S (S (S O))) + (S O)と読むことに注意してください。
演算子のほうが関数適用っぽいものより優先度が弱いです。
2*3を計算する例は,
S (S O) * S (S (S O)) = mult (S (S O)) (S (S O)) = S (S (S O)) + S O * S (S (S O)) = S (S (S O)) + S (S (S O)) + O * S (S (S O)) = S (S (S O)) + S (S (S O)) + O ... = S (S (S (S (S (S O)))))
という感じです。
Coqは便利で,具体的な例の計算ならやってくれます。
Theorem ex_2_plus_1_eq_3: S (S O) + S O = S (S (S O)). Proof. simpl. (* S (S O) + S O の部分を計算してくれる *) reflexivity. (* 両辺が同じ項の=となっているゴールを達成する *) Qed.
これで2 + 1が3であることを形式的に示すことができました!
証明tactic
ex_2_plus_1_eq_3の例では, 実際に証明を行っています。
coqでは定理の証明を次の形で書きます。
Threom 名前: 命題. Proof. 証明tacticの列 Qed.
Proof.のあとに続くのは証明のtacticというものです。 これは, 証明の状態を変化させます。
証明の状態とは, 証明するべきものである「ゴール」の列です。 ゴールとは次の形で表されます。
仮定の列 |- 結論
「仮定の列から結論を導く」ことを要求するものがゴールです。
始めに Theorem で示したい命題を与えると,
|- 命題
このように, 仮定の列が空で, 命題が結論となったゴールが1つだけ状態から始まります。 このゴールに対してtacticを適用することで, ゴールを変えたり, 達成したり, 増やしたりします。 そして, これらゴールをすべて達成すると, 証明を完遂したことになります。
Coqのインタラクティブツールで普通右側に表示されている状態は, この状態を表しています。
tacticをStep実行してみましょう
Theorem ex_2_plus_1_eq_3: S (S O) + S O = S (S (S O)). Proof. simpl. reflexivity. Qed.
例交えてやる。 TODO
taciticの一覧はここにあります TODO
証明
さて, 初めに示した命題の証明を行いたいと思います。
Definition task := forall n m, n * S m = n + n * m. Theorem solution: task. Proof. unfold task. (* FILL IN HERE *) Qed.
TODO
自動証明tactic
実はCoqのtacticは力強く, この程度の命題であれば自動で解いてくれる強いtaciticがあります。
自動証明tacticはゴールに対してtacticを適用するかを定義することで作られています。
例えばこの例では, ringというtacticを用いれば自動で行ってくれます。
他にも, auto, eauto, omegaといったtacticがあります。
しかしこれらは, 証明してくれる命題の範囲がそれほど広くないです。 それぞれのtacticの証明戦略を理解した上で, その証明を自分でもできるときに限って使うのが良いです。
僕が示せなかった証明を振り返る
長くなってきたので後編へ移ります。
Coqの勉強法はこれが一番有名らしいです。
わたしはこれやった https://t.co/lzg6cOnIPy
— そすうぽよ@技術書典 く54D (@_primenumber) 2019年8月21日
また京大の五十嵐先生の講義テキストも便利です。 Computation and Logic: Winter Semester 2018
最後に宣伝なのですが, 証明コンテストTopProverは出れば出るだけ得するレートの付き方をするらしいです。 是非参加して証明力を高めましょう。