wassup?

新ブログ→memo.wass80.xyz

DH鍵交換を手でやると変な事になった。DH鍵交換の素数は安全素数を選ぶ必要があるらしい。

開発

まとめ

現実逃避に、DH鍵交換を手でやってました。
手で試すと、運悪く不思議なケースを引きました。
調べると、DH鍵交換がうまく行かないケースは次の2つがあるようです。

  • パラメータpが安全素数でないこと。
  • p-1を共有してしまうこと。

失敗した手計算を共有します。
安全素数が良い理由については、まだ理解していないので書いてません。
理解していない部分を課題の形で置いてあります。

DH鍵交換とは?

DH(Diffie–Hellman)鍵交換は、2人で秘密の値を共有する方法です。
秘密の値は、秘密鍵暗号の鍵として利用されることが多いです。

https(TLS)でも利用できる手法です。
手順のわかりやすさから、RSAに並ぶおなじみの暗号手法です。

DH鍵交換の方法

DH鍵交換の方法をAさん、 Bさんの二人が行う様子で簡単に書きます。

巡回群 {\mathbb Z}/p{\mathbb Z}というのは、pで割った余りの世界を考えるということです。
群 {\mathbb Z}/p{\mathbb Z}において元 xの次数は、 x^ n = 1 \ ({\rm mod \ } p)を満たす最小の nのことを言います。
群 {\mathbb Z}/p{\mathbb Z}において元 xが生成元であるとは、次数がpであることを言います。

  • パラメータ (p, g)をAさんとBさんで共有する
  • 整数 aをAさんは p未満の数でランダムに決める
  • g^ a {\rm \ mod\ }p をAさんはBさんに共有する
  • 整数 bをBさんは p未満の数でランダムに決める
  • g^ b {\rm \ mod\ } p をBさんはAさんに共有する
  • Aさんは受け取った g^ bを a乗して、 K=(g^ b)^ a {\rm \ mod\ } pを得る
  • Bさんは受け取った g^ aを b乗する、 K'=(g^ a)^ b {\rm \ mod\ } pを得る

K = (g^ b)^ a = g^ { a b } = (g^ a)^ b = K'なので、AさんとBさんで同じ値を共有できました。

この通信を見ていたCさんは、 g^ aと g^ bを見ることができます。
これ同士を掛けてみても、得られるのは g^ {a + b}です。 g^ {ab}を求めたいのですが、行き詰まってしまいます。

Cさんは、 g^ aから aを求めるのが難しいという、離散対数問題に直面するわけです。

手計算でやってみる

パラメータの決定

とりあえず適当に素数と巡回群を決めればいいんだろうと、 p=83とg=2としました。
g=2はDH鍵交換で一般的なパラメータのようです。

2のn乗(mod 83)を求めていくと83乗で初めて1になります。 2は83の巡回群の生成元にちゃんとなっていました。

このp=83とg=2を通信先と共有しました。

g^ aを求める

僕は乱数を振ってa=46としました。
g^ a = 2^ {46} \ ({\rm mod\ }p) を計算しましょう。
繰り返し2乗法的なテクニックのおかげで、46乗は手でも簡単に求まります。

初めに 2^ 1, 2^ 2, 2^ 4, 2^ 8, 2^ {16}, 2^ {32}を計算します。
前の数を自乗していけば求まります。
2^ 1 = 2,\ 2^ 2=4,\ 2^ 4=16,\ 2^ 8=256=7,\ 2^ {16}=49,\ 2^ {32}=2401=77です。

そして、46を二進数に展開して掛けます。
g^ a = 2^ {46} = 2^ {2 + 4 + 8 + 32} = 2^ 2 * 2^ 4 * 2^ 8 * 2^ {32} = 4 * 16 * 7 * 77 = 51

g^ aが求まったので通信先に共有します。

K=(g^ b)^ aを求める

通信先からは g^ b = 82が帰ってきました。
K=(g^ b)^ a=82^ {46}を求めればDH鍵交換が完了します。

完了するはずでした。

82の46乗を同じテクニックで求めます。
すると、 82^ 2=1になってしまうことに気づきます。
そうなると、前の数を自乗して求めるので、 82^ 4, 82^ 8, 82^ {16}‥‥全部が1 になってしまいます。
つまり、82の偶数乗は1だし、奇数乗は 82^ 1だけになってしまい82です。
今回はa=46で偶数なのでK=1となりました。

通信先もK'=1が求まったようです。
これにて、秘密の値 K=1 を通信先と共有できました。
めでたしめでたし。

本当ですか?

DH鍵交換でp-1を共有したときに起こること

82^ nはnを変えても、1か82のどちらかにしかならないのは致命的な問題です。
攻撃者Cさんは秘密の値が1か82のどちらかでしかないことが、すぐに分かってしまいます。
どうしてこうなったのでしょう。

実は g^ aの結果がp-1になってしまうと、p-1は2乗すると常に1です。
つまり、次数が2になってしまうのでした。

(p-1)^ 2 = p^ 2 - 2p + 1 = 1 \ ({\rm mod \ } p)

これは大変です。
実は、p-1を共有しないように乱数でaとbを選ぶ必要があったということです。

課題1: 2が生成元のとき、 2^ {(p-1)/2}=p-1 \ ({\rm mod \ } p)は成り立つ?
そうであれば、 (p-1)/2を乱数を選ぶときに避ければいい。

p-1を共有しなければ大丈夫なのか

もし共有した値の次数が2に限らず、とても小さい次数だと大変です。
総当りで試すのが簡単になってしまいます。

実はp=83の場合、p-1と1以外の次数は41か82なのでした。
p-1を共有しなければ、大丈夫だったようです。
通信先から送られてきた g^ b = 82は、運が悪かったということです。

この、次数が小さくならないための条件が、pが安全素数であるということのようです。
pが安全素数であるとは、ある素数qを用いてp=2q+1と表せる素数のことです。

41が素数なので、83は安全素数です。
そのため、p-1以外の次数が大きかったようです。
pとして83を選べたことは運が良かったようです。

課題2: 安全素数だと1とp-1以外の次数は十分に大きい?

メモ:
CTFにおける離散対数問題に対するアプローチ - sonickun.log

φ(p)が小さい素因数に分かれるとダメということらしい。
安全素数だと、 φ(p)=p-1=2xpなので、都合が良さそううということはわかる。
直感的にはわかった。

応用数学６暗号方式 安永憲司 http://www-infosec.ist.osaka-u.ac.jp/~yasunaga/appmath6/encryption.pdf
で、安全素数である必要性を言及されています。
平方剰余である群が出てくるのですが、あんまり良くわかってません。

ちなみに、opensslで実装されている大きい安全素数pはここにあります。

github.com

研究も就活も何一つうまくできない。心が折れています。

感情

警告: 鬱的吐露

心が折れています。

つらい。

研究も就活も何一つうまくできない。

しんどい。

心を保てない。

今週もなにもできなかった。

現実逃避の行動を時々して、 それでかりそめの満足感を得てしまっている。

焼豚の写真です。

f:id:wass80:20211107203555p:plain

なぜ、1年で日の出の最も早い日は夏至の日ではないのか

知見

就活も研究もなにもかもうまくいっていないwassです。

ところで、夏至の日は1年で最も日の出ている時間が長いことが知られています。 しかし、1年で最も早く日の出る日は夏至の日ではないことはあまり知られていません。 国立天文台の暦Wikiに詳細が書かれています。

この事実を、太陽から見た地球の視点を補足しながら説明しようと思います。

暦Wiki/日の出入りと南中/日の出入りの季節変化 - 国立天文台暦計算室

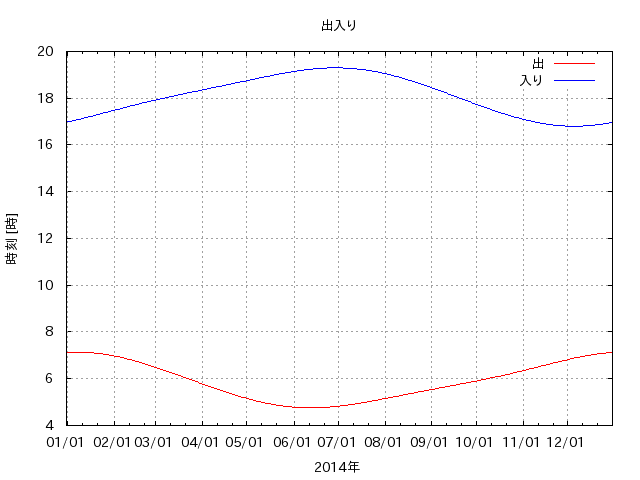
1年の日の出入りの変化は次のグラフに表されます。(この記事の全ての画像は暦Wikiより)

https://eco.mtk.nao.ac.jp/koyomi/wiki/C6FCA4CEBDD0C6FEA4EAA4C8C6EEC3E62FC6FCA4CEBDD0C6FEA4EAA4CEB5A8C0E1CAD1B2BDrsg3860_0.png

このグラフをみると、「日の入の遅くなるピーク」と「日の出の早くなるピーク」は半月ほどずれている事がわかります。なぜ、このようなことが起こるのでしょうか。

実は、日の出入りの時刻の複雑な変化は、南中時刻が季節に応じて変化するために起こります。夏至は一日が最も長くなりますが、南中時刻が遅くなっていく影響で、日の出が1番早い日は夏至の少し前なのです。

南中時刻が変化するということは、つまり実は、「太陽は常に正午に真南にくる」と言うのが嘘なのです。 これは日本標準時子午線のある明石市でも成り立ちません。

1日は1年を約365等分することで定義されています。 1日や正午の定義に南中時刻は関係ないため、南中時刻は1年のなかで微妙にずれることになります。

では、何が南中時刻の季節変化を引き起こしているのでしょうか。ここが非常に難しいです。

理由は2つあります。

  • 地球の公転する速度が一定ではないから。
  • 地球の自転軸の傾きにより、地球の自転の速度の公転方向の成分が増減するから。

地球の公転する速度は一定ではありません。 これは地球の公転軌道が楕円であるからです。

楕円軌道で太陽の周りをぐるぐる回る地球は、太陽に近い時は速く公転し、遠い時は遅く公転します。これは位置エネルギー+運動エネルギーが保存されることからわかります。

太陽から地球を眺めてみると、地球は1年で太陽の周りを回ります。そして、1年間に約366回、公転と同じ方向に自転しています。

太陽から地球をみると、 公転速度が一定であれば、今日と1日後には太陽からは同じ地球が見えます。 このとき、地球は公転の影響に追いつくため、自転を1回よりすこし余計に多く回っています。

実験してみましょう。自分の顔を太陽と思い、右手を地球として、右手を顔の横50cmのところに立ててみましょう。右手を見ると、手の側面が見えます。

このまま、自転せずに右手を顔の前に持ってくると、手の甲が見えます。 1日で公転を1/4回転した右手星が、1日分の自転をするためには、太陽に1日前と同じ右手を見せる必要があります。 そのため、右手首を1/4回す必要があることがわかります。 実際は1+1/4回だけ右手星は1日で自転します。 ただ、これを右手で再現すると右手がねじ切れるので気をつけましょう。

しかし、自転速度はそのままで、公転速度が速まると、地球は1日後の同じ時刻には同じ姿を見せてくれません。

公転速度が速まると、みかけの1日のために自転は余計に必要になります。自転が余計に必要ということは、地球から見ると太陽がなかなか上ってこないということです。そのため、南中時刻が遅れます。 逆に、公転速度が遅くなると、自転はすこしサボれます。そのため、南中時刻が早くなります。右手星を右斜め前や、左斜め前にもってくることで確かめることができます。

公転速度の変化による、南中時刻の変化は次のグラフに表されています。地球が太陽に近い1月を中心とした半年は、公転速度が速くなり、南中時刻は遅れていきます。 逆に地球が太陽から遠い7月を中心とした半年は、公転速度は遅くなり、南中時刻が早まっていきます。

https://eco.mtk.nao.ac.jp/koyomi/wiki/C6FCA4CEBDD0C6FEA4EAA4C8C6EEC3E62FC6EEC3E6BBFEB9EFA4CFCAD1B2BDA4B9A4EBB6D1BBFEBAB9A5B0A5E9A5D51.png

ところで、公転速度が一定であるとしても、南中時刻は変化します。 もう一つの要因である、自転軸の傾きの影響を考えてみましょう。

1日分地球が自転するには、公転の影響だけ、1回転と余計に自転する必要がありました。この影響は、公転面に対して一定です。 しかし、自転で一定に回転するのは赤道なのです。

地球の自転軸は23.4度ほど、公転面に対して傾いています。自転軸が傾いているということは、太陽から地球を見ると、地球の位置によって赤道の見え方も異なります。

太陽から地球の自転軸をみると、夏は自転軸が太陽側に傾いています。自転軸にともなって、赤道は手前側に傾いています。

手前側に傾いている赤道が回転した時、公転面への影響は拡大されて大きくなります。 すなわち、自転を余計にするとき、少し自転をサボることができます。自転をサボれるということは、南中時刻が早まります。

同様に、冬は自転軸が向こう側に傾いているので、同じように南中時刻が早まります。

// メモ: 公転速度の実験ぐらい直感的な実験が無いだろうか?

春と秋は赤道が右や左に傾いています。赤道が回転しても、公転面からは回転がすこしだけ遅く見えます。そのため、自転がさらに必要になります。南中時刻が遅れます。

自転軸の傾きの影響を南中時刻に反映したのが次のグラフです。夏と冬に早まり、春と秋に遅れる様子がわかります。

https://eco.mtk.nao.ac.jp/koyomi/wiki/C6FCA4CEBDD0C6FEA4EAA4C8C6EEC3E62FC6EEC3E6BBFEB9EFA4CFCAD1B2BDA4B9A4EBB6D1BBFEBAB9A5B0A5E9A5D52.png

これら、2つの要因を合成したものが、南中時刻の季節変化です。

興味深いことに、これら2つの要因による変動は同程度の影響があるため、どちらかを無視することは難しいです。

地球の公転速度の影響は14分ほどの増減で1年周期、自転軸の傾きの影響は20分ほどの増減で半年周期です。 結果として、sin波を2つ足し合わせたような南中時刻の変化が起こります。

https://eco.mtk.nao.ac.jp/koyomi/wiki/C6FCA4CEBDD0C6FEA4EAA4C8C6EEC3E62FC6EEC3E6BBFEB9EFA4CFCAD1B2BDA4B9A4EBB6D1BBFEBAB9A5B0A5E9A5D53.png

日の長さの計算と、南中時刻の計算を組み合わせることで、1年で最も日の出の早い日を計算できるということです。 難しいですね。

ところで、地球の楕円軌道も他の惑星の影響で変化しています。 また、地球の自転軸はそれ自体が公転面に対して回転しています。 そのため、上の南中時刻の変化のグラフも約21000年で変わっていくということです。スケールが大きいですね。

まとめ:

  • 日の出の最も早い日は夏至よりも10日ぐらい前。
  • その理由は南中時刻の季節変化。
  • 南中時刻の季節変化は、公転速度の変動や地軸の傾きの影響による。

参考:暦Wiki/日の出入りと南中/南中時刻は変化する - 国立天文台暦計算室

Dart 2の型を読む・void型に代入できる値とは?

Flutterに採用されているDartでは、void型に好きな値を代入することができます。

void main() {
  void x = 2;
}

型が値を定める言語に慣れていると、これは奇妙に思えます。しかし、型が振る舞いを定める言語であると思うと、これが自然と感じられるようになります。

ついでに、Dart 2の型の仕様書を読んでDartの型の上下を解説します。

と思って読んでたんですが、この仕様書はかなり不完全ですね‥。 Never型のこととかどこにも書かれていなかった‥。

仕様書 Dart 2.2

void型の振る舞い

型が値を定める言語では、voidは値の存在しない型となっています。そのため、voidの関数から値を返そうとするとコンパイルエラーになるし、void型の変数は存在できません。

Dartでは、void型は何の振る舞いもできない型となっています。任意の値は振る舞いをしない型として振る舞うことが可能です。そのため、Dartでは任意の値をvoid型に代入することができます。

一度void型に落ちた型は他の型に型変換ができなくなります。

Dartの型の一覧と仕様書の読み方

void型が任意の値を代入できるということを仕様書から読み解きます。

このときに、記号を3つほど知っている必要があります。

型S <: 型T は「型Sは型Tの派生型」であると読みます。また、派生型Sは元の型Tへ代入可能です。

記号の向きを忘れがちなのですが、|型S| < |型T| であるという雰囲気を感じ取りましょう。

型環境Γ |- 命題P は 「型環境Γにおいて命題Pを示せる」と読みます。

上下に命題が書かれた長い横棒は「上から下が導出できるとする」と読みます。

次の導出木は、上に何も書かれていないので、いつでも成り立つということを述べています。

f:id:wass80:20210408132757p:plain

つまり、任意の型Sは任意の型Sとして振る舞うことができると言っています。当然ですね。

Object型 Dynamic型 void型

f:id:wass80:20210408132945p:plain

Object型 Dynamic型 void型は任意の値を代入できます。それぞれの実際の振る舞いは型の導出木には現れていません。

Object型は==ができます。

Dynamic型は何でもできる型です。 動的に様々なチェックがなされます。

void型は何もできない型です。 何かをするとコンパイルエラーです。

⊥型(ボトム型)

f:id:wass80:20210408133414p:plain

数学には現れにくいが、計算機科学だと頻出する⊥型です。

⊥型はループや例外などにより値を返さない関数につく型です。

例えば、「intを受け取って⊥を返す関数」は実際には値を返しません。 値を返さない関数は「任意の型を返す関数」として、型推論時は振る舞うことができます。

⊥型を明示的にコード内で記述する場合は Never が使えます。

Null型

f:id:wass80:20210408133426p:plain

Null型は⊥型以外のすべての型の派生型であると述べています。

ですがこれは悲しいので、null-safetyモードの場合はObject?の派生型でしかなくなるようです。

understanding null-safety

Rassbery PIにつけたタッチスクリーンのキャリブレーションをする

Rassbery PI Zero Wにタッチスクリーンを付けました．

買ったのはこのKINCREAの7インチスクリーンです．

KINCREA 7インチ Raspberry Pi用 ディスプレイ 1024 * 600解像度 ホルダー付き Raspberry Pi 4 3 B+ 3 2に適用 HDMI入力 タッチパネル タッチスクリーン モニター HD ラズベリーパイ JC711

KINCREA 7インチ Raspberry Pi用 ディスプレイ 1024 * 600解像度 ホルダー付き Raspberry Pi 4 3 B+ 3 2に適用 HDMI入力 タッチパネル タッチスクリーン モニター HD ラズベリーパイ JC711

  • メディア: エレクトロニクス

HDMIで画面が光り，USBでタッチスクリーンが動きます，

ただ，タッチスクリーンの左端の少しだけが反応しませんでした．
直すために，補正の設定が必要になります．

キャリブレーションの方法

ドライバのevdev，キャリブレーション用のアプリxinput_calibratorを入れる．

 $ sudo apt install -y xserver-xorg-input-evdev xinput_calibrator

xinput_calibratorを起動して，calibにキャリブレーション情報を保存する

$ DISPLAY=:0 xinput_calibrator --misclick 0 > calib

十字をタッチします．
画面の左側が反応しないので，左の十字は右よりでタッチします． f:id:wass80:20200923235814p:plain

calibの情報をもとに， /usr/share/X11/xorg.conf.d/99-calibration.confにキャリブレーション情報を書き込む．

$ cat calib
Calibrating EVDEV driver for "wch.cn USB2IIC_CTP_CONTROL" id=6
    current calibration values (from XInput): min_x=181, max_x=4009 and min_y=59, max_y=4000

Doing dynamic recalibration:
    Setting calibration data: 267, 3933, 49, 3833
    --> Making the calibration permanent <--
  copy the snippet below into '/etc/X11/xorg.conf.d/99-calibration.conf' (/usr/share/X11/xorg.conf.d/ in some distro's)
Section "InputClass"
  Identifier  "calibration"
  MatchProduct    "wch.cn USB2IIC_CTP_CONTROL"
  Option  "Calibration" "267 3933 49 3833"
  Option  "SwapAxes"    "0"
EndSection
$ sudo vi -p /usr/share/X11/xorg.conf.d/99-calibration.conf  calib

/usr/share/X11/xorg.conf.d/99-calibration.confの内容

Section "InputClass"
        Identifier      "calibration"
        MatchProduct    "wch.cn USB2IIC_CTP_CONTROL"
        Driver "evdev"
        Option  "Calibration"   "260 3933 49 3870"
EndSection

Driver "evdev"は明示的に必要でした．

Option "Calibration" "260 3933 49 3870"は"x-min x-max y-min ymax"．
手で数値をいじるときは，ポインタがはみ出すなら値の区間を広くすれば良いです．

最後に再起動しましょう．

$ sudo reboot

xinput_calibratorの内容はドライバの設定によって変化します．
うまく行かない場合は99-calibration.confの設定を書き換えて再起動を試してください

xorgの挙動を調べる

xinput listでデバイスネームやidを調べられます．

pi@raspberrypi:~ $ DISPLAY=:0 xinput list
⎡ Virtual core pointer                        id=2    [master pointer  (3)]
⎜   ↳ Virtual core XTEST pointer                id=4    [slave  pointer  (2)]
⎜   ↳ wch.cn USB2IIC_CTP_CONTROL                id=6    [slave  pointer  (2)]
⎜   ↳ Logitech USB Optical Mouse                id=7    [slave  pointer  (2)]
⎣ Virtual core keyboard                       id=3    [master keyboard (2)]
    ↳ Virtual core XTEST keyboard                 id=5    [slave  keyboard (3)]

xinput list-propsで設定されているプロパティを確認できます．
ここに値がなければ正しく設定されていません．

pi@raspberrypi:~ $ DISPLAY=:0 xinput list-props 6
Device 'wch.cn USB2IIC_CTP_CONTROL':
    Device Enabled (114):   1
    Coordinate Transformation Matrix (115): 1.000000, 0.000000, 0.000000, 0.000000, 1.000000, 0.000000, 0.000000, 0.000000, 1.000000
    Device Accel Profile (240): 0
    Device Accel Constant Deceleration (241):   1.000000
    Device Accel Adaptive Deceleration (242):   1.000000
    Device Accel Velocity Scaling (243):    10.000000
    Device Product ID (244):    6790, 58851
    Device Node (245):  "/dev/input/event1"
    Evdev Axis Inversion (246): 0, 0
    Evdev Axis Calibration (247):   260, 3933, 49, 3870
    Evdev Axes Swap (248):  0
    Axis Labels (249):  "Abs MT Position X" (238), "Abs MT Position Y" (239), "Abs MT Touch Major" (237), "None" (0), "None" (0)
    Button Labels (250):    "Button Unknown" (234), "Button Unknown" (234), "Button Unknown" (234), "Button Wheel Up" (120), "Button Wheel Down" (121)
    Evdev Scrolling Distance (251): 0, 0, 0
    Evdev Middle Button Emulation (252):    0
    Evdev Middle Button Timeout (253):  50
    Evdev Middle Button Button (254):   2
    Evdev Third Button Emulation (255): 1
    Evdev Third Button Emulation Timeout (256): 750
    Evdev Third Button Emulation Button (257):  3
    Evdev Third Button Emulation Threshold (258):   1000
    Evdev Wheel Emulation (259):    0
    Evdev Wheel Emulation Axes (260):   0, 0, 4, 5
    Evdev Wheel Emulation Inertia (261):    10
    Evdev Wheel Emulation Timeout (262):    200
    Evdev Wheel Emulation Button (263): 4
    Evdev Drag Lock Buttons (264):  0

evdevの設定名は man evdev で確認できます．

list-propsで表示されているプロパティ名とxorgsのconfの設定名は異なります．
気をつけましょう．

長押し右クリックはうまくいかない

evdevで長押ししたときの挙動を右クリックにできるようなのですが，うまくいきませんでした．謎．
この設定で動くと思うんだけどな

        Option  "EmulateThirdButton"            "1"
        Option  "EmulateThirdButtonTimeout"     "750"
        Option  "EmulateThirdButtonMoveThreshold"   "30"

タッチスクリーンのセットアップ

買ったタッチスクリーンは次の3口を持っています.

  • HDMI
  • USB type B micro 外側 タッチスクリーンデバイス
  • USB type B micro 内側 給電のみ

Raspi Zero Hは次の3口を持っています

  • miniHDMI
  • USB type B micro 内側 デバイス用
  • USB type B micro 外側 給電のみ

買ったタッチスクリーンには次のものが付属しました．

これはタッチスクリーンがRaspiB用のためだからです． なので，Zeroを接続するために追加で必要なものは次の2つです．

これらと，給電用のUSBケーブル+AC/DCが必要です．

3本のケーブルで動作しました．

  1. HDMIケーブルををスクリーンにつなぎ，HDMIを変換してHDMI microにしてRaspiにつなぐ
  2. 給電typeB microケーブルをスクリーンの内側に刺す
  3. もう1本のUSBケーブルをスクリーンと，typeB micro変換してraspiの内側につなぐ (同時にraspiに給電される)

感想

変換器にお金が必要なので，それならば，もともと対応していたraspiのBを買えばよかったなと思いました．

GPIOピンとlinuxが必要でなければ，安いタブレットを買ったほうが便利だと思います．

ISUCON10 予選参加 (24位 team😇😇😇)

ISUCON10の予選にteam😇😇😇で参加しました．

結果は24位で通過です．めでたい

やったこと

計測

  • new relic
    • どのrequestが遅いとか，sqlが何回何秒かかってるかわかって便利だった．
  • sql slow log
    • indexが効いてないクエリがたくさん確認できた
    • utgwがforce indexでちまちまindexを適用していた
  • access log
    • utgwがsearch系の検索クエリの種類の統計をとってくれた
    • featuresは2-3回しかクエリが飛んでこないので無視でOK

運用

  • 1台go 2台mysqlで実装
  • 独立したmysqlで両方に同じinsertをした．
  • 乱数ラウンドロビンでselectを分散した．

  • その他色々チューニングをnonyleneがしてくれた．

  • chairとestateの垂直分割が正着っぽい‥

N+1改善

  • nazotteの多角形内部の座標にあるestateをselectがN+1だった
  • 多角形内部の判定をする前に，凸包する矩形で多めにestateをとってきて， 一つ一つ内側か判定していた．
  • 単に一つのクエリにまとめることができる．
  • 10倍ぐらい速くなって，少なくともボトルネックではなくなった．

https://github.com/innocent-team/isucon10q/commit/051ece1bb50e3b23c4ae2f49de9c2f75bc8e7f4f (そのうち公開)

SELECT * FROM estate
    WHERE latitude <= ? AND latitude >= ?
    AND longitude <= ? AND longitude >= ?
    AND ST_Contains(ST_PolygonFromText(?), POINT(latitude, longitude))
    ORDER BY popularity DESC, id ASC
    LIMIT ?

できなかったこと

  • low_pricedのキャッシュを実装したが，効果がなくrevert．
  • 唯一のupdate要素のchair.stockをDBから引き剥がす実装もしたが，こっちはfailedしたの諦め．

感想

  • 今年はgolang書くのにすでになれていたので，実装で困ることは少なかった．
  • ISUCONのための言語だなとつくづく思う
  • ちゃんと一番重大なボトルネックから順番に対処できてよかったと思う．